Gibbs–Thomson equation

The Gibbs–Thomson effect in physics refers to the observation that small crystals of a liquid melt at a lower temperature than the bulk liquid. The melting point depression is inversely proportional to the pore size, as given by the Gibbs–Thomson equation.

Contents

Introduction

The technique is closely related to using gas adsorption to measure pore sizes, but uses the Gibbs–Thomson equation rather than the Kelvin equation. They are both particular cases of the Gibbs Equations of Josiah Willard Gibbs: the Kelvin equation is the constant temperature case, and the Gibbs–Thomson equation is the constant pressure case.[1]

This behaviour is closely related to the capillary effect and both are due to the change in bulk free energy caused by the curvature of an interfacial surface under tension.[2][3]

The original equation only applies to isolated particles, but with the addition of surface interaction terms (usually expressed in terms of the contact wetting angle) can be modified to apply to liquids and their crystals in porous media. As such it has given rise to various related techniques for measuring pore size distributions, see Themoporometry and Cryoporometry.

The Gibbs–Thomson effect lowers both melting and freezing point, and also raises boiling point. However, simple cooling of an all-liquid sample usually leads to a state of non-equilibrium super cooling and only eventual non-equilibrium freezing. To obtain a measurement of the equilibrium freezing event, it is necessary to first cool enough to freeze a sample with excess liquid outside the pores, then warm the sample until the liquid in the pores is all melted, but the bulk material is still frozen. Then, on re-cooling the equilibrium freezing event can be measured, as the external ice will then grow into the pores.[4][5] This is in effect an "ice intrusion" measurement (cf. Mercury Intrusion), and as such in part may provide information on pore throat properties. The melting event can be expected to provide more accurate information on the pore body.

The geometry of the crystal–liquid interface determines the value of the constant in the Gibbs-Thomson equation – the conventional "4" only applies to a spherical interface in a cylindrical pore.

Gibbs–Thomson equation for particles

For an isolated spherical solid particle of diameter x in its own liquid, the Gibbs-Thomson Equation for the structural melting point depression can be written:[6]

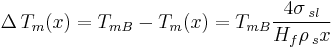
\Delta\,T_m(x)=T_{mB}-T_m(x)=T_{mB}\frac{4\sigma\,_{sl}}{H_f\rho\,_sx}

Where: TmB=Bulk Melting temperature

σsl = solid–liquid interface energy (per unit area)
Hf = bulk enthalpy of fusion (per gram of material)
ρs = density of solid

The "4" in the above equation comes from the spherical geometry of the solid-liquid interface.

Note: x is used for the pore size rather than d for a number of reasons :

It is consistent with the original published notation.
The equation can be used with planar geometry (with a change of constant).
For consistency with the related Strange–Rahman–Smith equation where the symbol d is used for the differential operator.

Gibbs–Thomson equation for liquids in pores

Very similar equations may be applied to the growth and melting of crystals in the confined geometry of porous systems. However the geometry term for the crystal-liquid interface may be different, and there may be additional surface energy terms to consider, which can be written as a wetting angle term 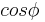cos\phi\,. The angle is usually considered to be near 180°. In cylindrical pores there is some evidence that the freezing interface may be spherical, while the melting interface may be cylindrical, based on preliminary measurements for the measured ratio for 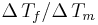\Delta\,T_f / \Delta\,T_m in cylindrical pores.[7]

Thus for a spherical interface between a non-wetting crystal and its own liquid, in an infinite cylindrical pore of diameter x, the structural melting point depression is given by:

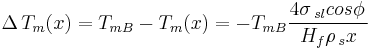
\Delta\,T_m(x) = T_{mB}-T_m(x)= - T_{mB}\frac{4\sigma\,_{sl}cos\phi\,}{H_f\rho\,_sx}

Simplified Gibbs-Thomson equation

The Gibbs-Thomson equation may be written in a compact form:[8]

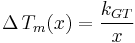
\Delta\,T_m(x)= \frac{k_{GT}}{x}

where the Gibbs-Thomson Coefficient 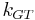k_{GT} assumes different values for different liquids [6][7] and different interfacial geometries (spherical/cylindrical/planar).[7]

In more detail:,[1][9]

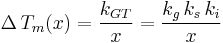
\Delta\,T_m(x)= \frac{k_{GT}}{x} = \frac{k_g \, k_s \, k_i}{x}

Where : 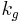k_g is a geometric constant dependent on the interfacial shape,

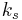k_s is a constant involving parameters specific to the crystalline solid of solid–liquid system, and
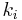k_i is an interfacial energy term.

Origins of the Gibbs–Thomson equation

Josiah Willard Gibbs has deservedly given his name to the first part of this equation, as it a particular case of his generalised Gibbs Equations.[10]

It is somewhat less clear where the "Thomson" part came from. The easy assumption is that it was William Thomson, who later as Lord Kelvin gave his name to the Kelvin equation. However, it was probably experiments by his brother James Thomson (also known for his innovations in the analysis of regelation – the effect of pressure on the freezing point of water) that originated the subject. There are recorded letters between Gibbs and the two Thomson brothers on these subjects. However the original version of the Gibbs-Thomson equation appears to occur in J. J. Thomson's book on "generalised dynamics", on page 258 (but the notation is very different).[11] Thus all three Thomsons appear to share the honours. [12]

References

  1. ^ a b Mitchell, J.; Webber, J. Beau W.; Strange, J.H. (2008). "Nuclear Magnetic Resonance Cryoporometry". Phys. Rep. 461: 1–36. Bibcode 2008PhR...461....1M. doi:10.1016/j.physrep.2008.02.001. 
  2. ^ Defay, R.; Prigogine, I.; Bellemans, A.; Everett, D.H. (1951 reprinted 1966), Surface tension and adsorption, Longmans Green and Co. 
  3. ^ Gregg, S.J.; Sing, K.S.W. (1967), Adsorption surface area and porosity (second edition ed.), Academic Press 
  4. ^ Petrov, O.; Furo, I. (Jan 2006), "Curvature-dependent metastability of the solid phase and the freezing-melting hysteresis in pores", Phys. Rev. 73 (1): 7, ISSN 1539-3755 
  5. ^ Webber, J. Beau W.; Anderson, Ross; Strange, John H.; Tohidi, Bahman (2007), "Clathrate formation and dissociation in vapour/water/ice/hydrate systems in SBA-15 Sol-Gel and CPG porous media as probed by NMR relaxation novel protocol NMR Cryoporometry Neutron Scattering and ab-initio quantum-mechanical molecular dynamics simulation.", Magn. Reson. Imaging (Elsevier) 25 (4): 533–536, doi:10.1016/j.mri.2006.11.022, PMID 17466781 
  6. ^ a b Jackson, C. L.; McKenna, G. B. (Dec 1990), "The melting behavior of organic materials confined in porous solids", J. Chem. Phys. 93 (12): 9002–9011, Bibcode 1990JChPh..93.9002J, doi:10.1063/1.459240, ISSN 0021-9606 
  7. ^ a b c Webber, J. B. W. (2010), "Studies of nano-structured liquids in confined geometries and at surfaces", Progress In Nuclear Magnetic Resonance Spectroscopy 56 (1): 78–93, doi:10.1016/j.pnmrs.2009.09.001 
  8. ^ Strange, J.H.; Rahman, M.; Smith, E.G. (Nov 1993), "Characterization of Porous Solids by NMR", Phys. Rev. Lett. 71 (21): 3589–3591, Bibcode 1993PhRvL..71.3589S, doi:10.1103/PhysRevLett.71.3589, PMID 10055015, http://link.aps.org/doi/10.1103/PhysRevLett.71.3589 
  9. ^ Webber, J. Beau W.; Dore, John C.; Strange, John H.; Anderson, Ross; Tohidi, Bahman (2007), "Plastic ice in confined geometry: The evidence from neutron diffraction and NMR relaxation.", J. Phys.: Condens. Matter 19: 415117 (12pp), Bibcode 2007JPCM...19O5117W, doi:10.1088/0953-8984/19/41/415117, http://stacks.iop.org/0953-8984/19/415117 
  10. ^ Gibbs, J. W (1928), The collected works of J. Willard Gibbs, Longmans Green and Co. 
  11. ^ Thomson, J.J. (1888), Applications of dynamics to physics and chemistry, Macmillan and Co. 
  12. ^ Webber, Beau; Dore, John (2004), "Structural and Dynamic Studies of Water in Mesoporous Silicas using Neutron Scattering and Nuclear Magnetic Resonance", J. Phys.: Condens. Matter (IoP) 16 (Special Issue: Water in Confined Geometry): S5449-S5470, Bibcode 2004JPCM...16S5449W, doi:10.1088/0953-8984/16/45/009, http://stacks.iop.org/JPhysCM/16/S5449